Running Tangents
Running Tangents
What is a tangent, what do they have to do with running and why should you care about running them?

The red straight line here is the tangent, touching but not crossing the black curved line at the point of the red dot.
Firstly, what is a tangent?
In geometry, a tangent is “a straight line touching a curve at a single point without crossing it there”. Easy, right?
Ok… but what do they have to do with running?
In its strict definition, not much, but the term “running tangents” has become effectively synonymous with “running the racing line” which does have relevence if you are trying to run your fastest time in a race.
The racing line
A race is measured out to be exactly the advertised length, but most runners will run further than that. Why? Because the course is measured along the shortest line possible, this is often called the “racing line”.
The shortest distance between two points is a straight line so to run that shortest distance, you need to run straight wherever possible – and wherever possible is anywhere not going around a corner. This includes running diagonally between opposite corners rather than following one side of the course of the other.
Why should you care?
Because, despite the course being an exact distance, running that exact distance relies on it being run the way it was measured, any deviation from this line will add to the total distance.
If you want to run your fastest time, maybe get that new PB, then you’ll want to make sure you run the shortest route possible and no, that doesn’t mean taking short cuts!
Most people won’t run the optimal racing line, or more specifically, they can’t run the optimal racing line.
When there are large number of runners in a group, they need to spread out across the course. This happens more nearer the start of a race until runners start to spread out. Many also prefer a bit of space rather than running crammed up against someone else even when the road isn’t that busy.
 Max Alexander / PromoMadrid [CC BY-SA 2.0], via Wikimedia Commons
Max Alexander / PromoMadrid [CC BY-SA 2.0], via Wikimedia Commons
Having a lot of runners in a small space causes congestion which stops them all from being able to freely move side-to-side across the course and are unable to run the optimal racing line.

Here, the blue line represents the racing line around this corner; the shortest route. Only those running in enough space that they can freely move sideways will be able to follow this line.
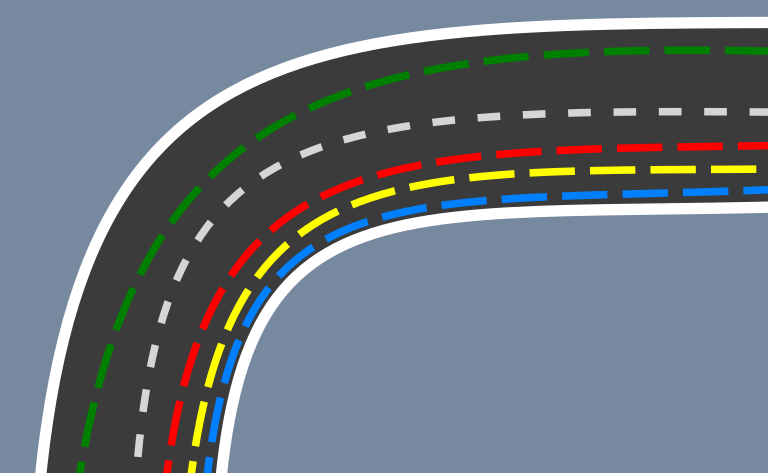
Compare the racing line to some examples of how someone might run around the corner. Red and Yellow are running side-by-side, maybe in the middle of a group, which causes Red to have to run wider, increasing the distance travelled.
Green is shown as an example of someone running at the edge of a congested group and having to run very wide involving much more distance.
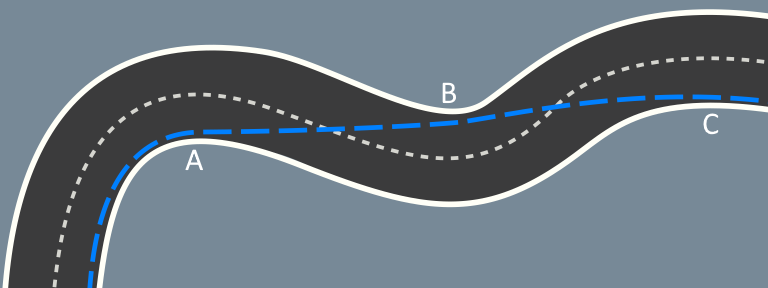
This is a longer example involving multiple corners, note that the racing line here is almost a straight line from corners A to C.
A straight line between A and C that just touches B would be a tangent to the curve at B, hence “running tangents”!
This is where we get the term “running tangents” but an actual tangent isn’t something that happens often so the term tends to apply to running the racing line in general.
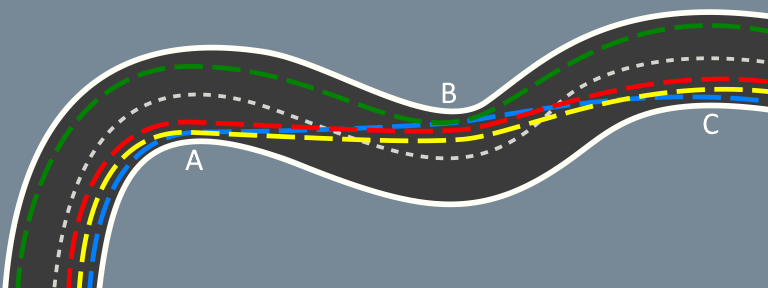
Again, with the same runners where Red and Yellow both run a slightly longer distance, neither able to follow the racing line. While Green, again out at the edge of this group, runs the furthest.
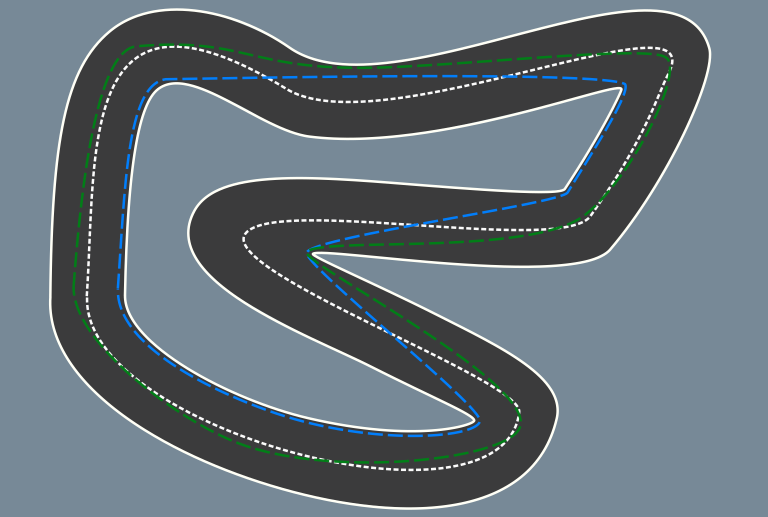
In this loop, notice how the blue racing line cuts diagonally across the track between turns to run close around each one, and also how along the top section the it is actually a straight line between A and C, not touching point B.
Our poor green runner is yet again stuffed out to the side because of other runners around so will end up running much further than needed.
 Stephen McKay / BUPA Great Birmingham Run [CC BY-SA 2.0]
Stephen McKay / BUPA Great Birmingham Run [CC BY-SA 2.0]
An example of runners spreading across the course. The racing line would be close to the painted double-yellow lines along the inside (left) edge of the road, but these runners want some space rather than all being squashed up close to that line.
Does it really matter that much?
At 2-hour half marathon pace, 100 metres will take 34 seconds so running an extra 400 metres will increase your time by over 2 minutes! If you were coming in at 1:59 when you have run 21.1k then you are going to end up finishing the race just after 2:01 as that sub-2-hour finish slips past. Did you run 21.1k in under 2 hours? Sure! But did you finish that half marathon in under 2 hours? Sadly not, and that is the official time and the one that matters to most.
To find out roughly how much extra distance are we talking about, we can start off by using an accurately measured route - an athletics track. The length of lane 1 is 400 metres (measured 30cm from the inside) and each lane outside it is longer.

The difference in lane lengths is why track races over 100m have staggered starts. Everyone will run the same distance by the finish line.
Distances for each lane in metres:
- Lane 1: 400
- Lane 2: 407.67
- Lane 3: 415.33
- Lane 4: 423
- Lane 5: 430.66
- Lane 6: 438.33
- Lane 7: 446
- Lane 8: 453.66
Each lane is 7.67 metres longer than the one inside it.
A 10k round a track is 25 laps, but that assumes running on the inside lane. Running the same number of laps in lane 2 will add on 191.67 metres to the distance compared to lane 1, almost half a lap extra from being just 1.22 metres (width of a track lane) wider.
Things aren’t so easy to calculate when out on the road though as there is as every course is different and most of the corners taken within that course are also different!
Example: London Marathon, Cutty Sark
A good example from a famous race, going around the Cutty Sark during the London Marathon. This is just after the 60k/6mile mark, so the crowds haven’t yet thinned out and lots of runners are bunched up together, spreading them across the course and making running the racing line impossible (without pushing everyone out of the way!).
 Twitter @LondonMarathon
Twitter @LondonMarathon
The turn is a big U-bend (or 2 right angle turns right after each other if you prefer) where the racing line will be up against the barrier on the inside (closest to the ship) but as there are so many runners there together, a lot will be running wide to find some space.
And spreading out like this makes a big difference to how far those runners on the outside of the corner are running compared to those on the inside.
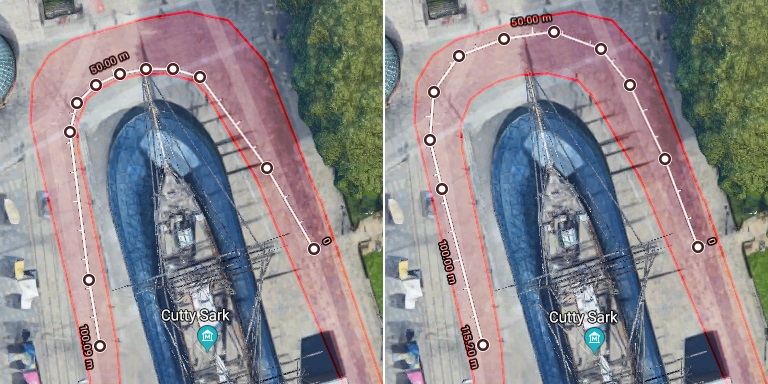
The red shaded area is the guesstimated course from the previous photo. The left image shows the distance when following close to the racing line with a 100m long section measured. The right image shows the same start and end points, but the route is one that may have to be taken when running amongst with a busy crowd. You would need to run 15 metres further on this line than someone following the racing line. That’s a pretty extreme example to highlight the effect but some people will end up running this line. Even following the middle of the road round this bend adds on 8-10 metres for just this corner – many will run this line.
Example: Right angled road turning
Even a standard right-angle corner on an average road can have up to 10 metres added to it by running the outside of the bend.
This example, again taken from the London Marathon course (though not in the last few years) is a nice right angle.
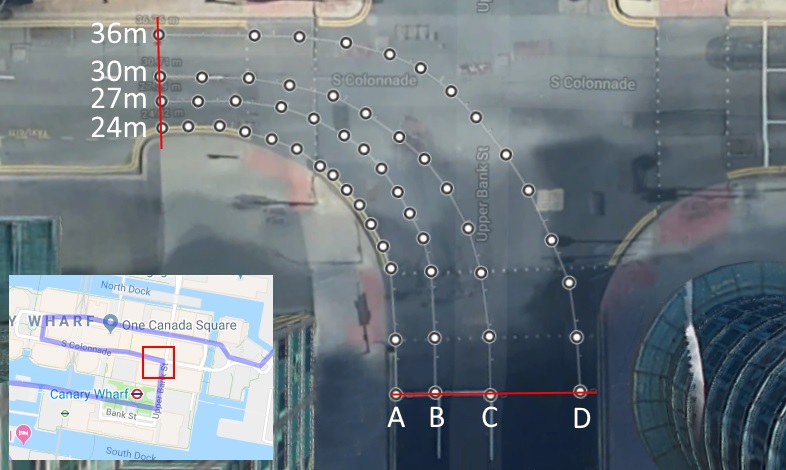
The line A is the racing line and measures the corner to 24 metres, each of B, C and D are wider lines, starting and finishing level with each other. Line B adds on 3 metres to the distance of this bend, line C another 3 (6 in total) and line D, a massive 12 metres longer!
Notice on distance calculations: Yes, the calculations here are done using Google Maps, I know that this isn’t a very accurate method but the goal here isn’t to give exact distances for any given corner/course but to give a general guide. For this purpose, this method is accurate enough.
To see this proper measurements, check out this post by DC Rainmaker.
Also, see page 21 of the IAAF-AIMS booklet The Measurement of Road Race Courses for example suggesting a 10m wide road can add on 12m by following the outside of the turn.
And how many corners are there in a race? Obviously all races are different but a race with just 20 corners, you could be adding on 200 metres by running the outside of each one. Not that someone will run the outside of every corner as they will be on the inside of as many as the outside, but long races have many bends and many opportunities to run a longer distance.
You can't run a shorter distance than the race length, but you can easily run longer!
How much further than the race distance do you think you ran in your last race by running wide round corners?
